ទ្រឹស្តីបទមេដ្យាន

ទ្រឹស្តីបទមេដ្យាន គឺជាទ្រឹស្តីបទសិក្សាពីទំនាក់ទំនងរវាងរង្វាស់មេដ្យាននៃត្រីកោណនិងរង្វាស់ជ្រុងនិមួយៗរបស់វា។ ទ្រឹស្តីបទមេដ្យានជាករណីពិសេសរបស់ទ្រឹស្តីបទអាប៉ូឡូនុស (Apollonius' theorem) ។

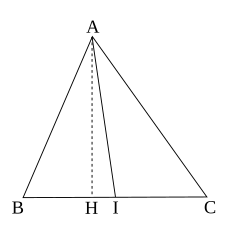
ទ្រឹស្តីបទមេដ្យាន

គេមានត្រីកោណ ABC ដែល AI ជារង្វាស់មេដ្យានគូសចេញពីកំពូល A ។ គេបានទំនាក់ដូចខាងក្រោម:

AB^{2}+AC^{2}=2BI^{2}+2AI^{2}\,

ឬ

AB^{2}+AC^{2}={1 \over 2}BC^{2}+2AI^{2}\,

បំណកស្រាយទ្រឹស្តីបទ

លក្ខណៈនេះជាករណីធម្មតាដោយការកាត់បន្ថយនៃអនុគមន៍ស្តាលែរលេបនីស្ស (scalar function of Leibniz):

AB^{2}+AC^{2}=({\overrightarrow {AI}}+{\overrightarrow {IB}})^{2}+({\overrightarrow {AI}}+{\overrightarrow {IC}})^{2}

គេពន្លាត:

AB^{2}+AC^{2}=AI^{2}+IB^{2}+2{\overrightarrow {AI}}.{\overrightarrow {IB}}+AI^{2}+IC^{2}+2{\overrightarrow {AI}}.{\overrightarrow {IC}}

ចំនុច I ជាចំនុចកណ្តាល [BC] ដូចនេះ ${\overrightarrow {IB}}$ និង ${\overrightarrow {IC}}$ មានទិសដៅផ្ទុយគ្នា និង $IC^{2}=IB^{2}$ ដូច្នេះ

AB^{2}+AC^{2}=2AI^{2}+2IB^{2}\,

បំណកស្រាយម្យ៉ាងទៀត

តាង H ជាចំណោលនៃកំពស់ត្រីកោណពីកំពូល A មកលើជ្រុង BC ចែកត្រីកោណ ABC ជាពីរត្រីកោណកែង BHA និង AHC ។ ដោយអនុវត្តទ្រឹស្តីបទពីតាករ គេបាន

AB^{2}=BH^{2}+AH^{2}\,

AC^{2}=AH^{2}+HC^{2}\,

AI^{2}=IH^{2}+AH^{2}\,

ហេតុនេះ

AB^{2}+AC^{2}=BH^{2}+2AH^{2}+HC^{2}\,

ដោយសំដែង BH និង HC ជាអនុគមន៍នៃ BI និង IH (ដែល I ជាចំនុចគណ្តាលនៃ BC និង BI=IC) ។ កត់សំគាល់ផងដែរចំពោះករណីពិសេស ជើង H នៃកំពស់គូសចេញពីកំពូល A មកលើអង្កត់ [BI] នៅចន្លោះ B និង I ប៉ុន្តែវាផ្ទៀងផ្ទាត់គ្រប់ករណី

BH=BI-IH\,

HC=IC+IH=BI+IH\,

ជំនួសចូលក្នុងកន្សោមខាងលើ គេបាន

AB^{2}+AC^{2}=(BI-IH)^{2}+2AH^{2}+(BI+IH)^{2}\,

AB^{2}+AC^{2}=BI^{2}-2BI.IH+IH^{2}+2AH^{2}+BI^{2}+2BI.IH+IH^{2}\,

AB^{2}+AC^{2}=2BI^{2}+2IH^{2}+2AH^{2}=2BI^{2}+2(IH^{2}+AH^{2})\,

ឬគេអាចថា

IH^{2}+AH^{2}=AI^{2}\,

ដោយជំនួសវាចូលក្នុងសមីការខាងលើគេបាន

AB^{2}+AC^{2}=2BI^{2}+2AI^{2}\,

ទ្រឹស្តីបទទី៣នៃមេដ្យាន

ជាមួយនឹងផលគុណស្កាលែរ: $AB^{2}-AC^{2}=2{\overrightarrow {BC}}.{\overrightarrow {IH}}$ ដែល H គឺជាចំណោលកែងនៃ A លើ (BC) ។

ដែលទំនាក់ទំនង $\left|AB^{2}-AC^{2}\right|=2BC\times IH$ (ទ្រឹស្តីបទទី៣នៃមេដ្យាន)។

តាមពិត: $AB^{2}-AC^{2}=({\overrightarrow {AB}}+{\overrightarrow {AC}}).({\overrightarrow {AB}}-{\overrightarrow {AC}})=2{\overrightarrow {AI}}.({\overrightarrow {AB}}+{\overrightarrow {CA}})=2{\overrightarrow {AI}}.{\overrightarrow {CB}}$

ចំណោលនៃ ${\overrightarrow {AI}}$ លើ ${\overrightarrow {BC}}$ គឺ ${\overrightarrow {HI}}$ ដែល ${\overrightarrow {AI}}{\overrightarrow {CB}}={\overrightarrow {HI}}.{\overrightarrow {CB}}={\overrightarrow {BC}}.{\overrightarrow {IH}}$ ។